Understanding word2vec
Machine Learning for Dummies
Arnaud Bailly
2016-09-05
Motivation
Caveat Emptor
All humans have equal intelligence;
Every human has received from God the faculty of being able to instruct himself;
We can teach what we don’t know;
Everything is in everything.
Joseph Jacotot (1770-1840)
It all started…
as a silly coding challenge to apply for a job:
Extract the top 400 articles from Arxiv corresponding to the query
big data, analyze their content using Google’s word2vec algorithm, then run a principal component analysis over the resulting words matrix and display the 100 most frequent words’ position on a 2D figure. In Haskell…
Understanding ML
- Going beyond tools
- Going beyond (obscure) mathematical formulas and theoretical principles
- Acquire intuitions about how ML works and can be used
Challenges
- To understand how word2vec works
- To optimize word2vec for large data sets
- To complete a data analysis pipeline
Understanding Basic word2vec Algorithm
Demo
Principles
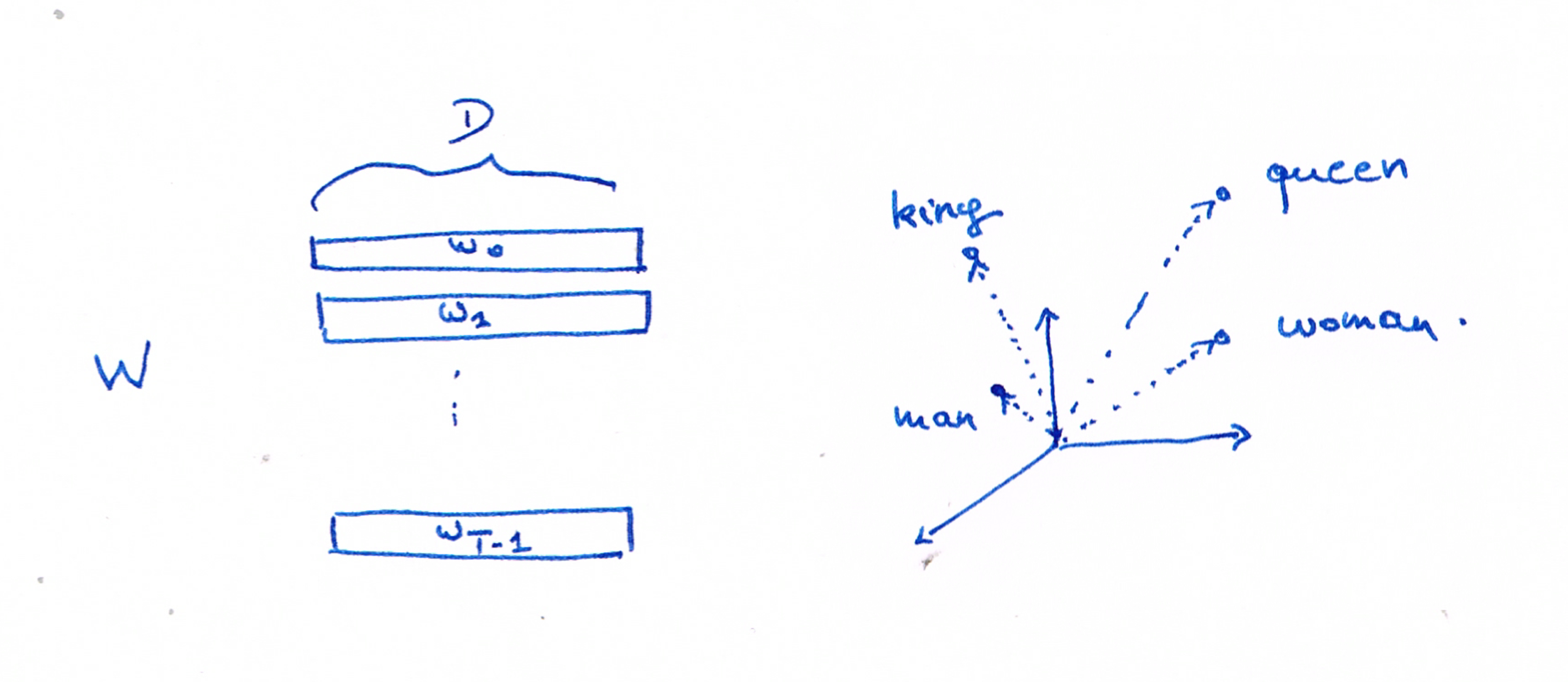
- Goal: Build a words embedding model, e.g. a function \(e: W \rightarrow R^d\) that maps each word from a given vocabulary \(W\) to a high-dimensional vector space
- Word2vec is actually more a family of
models:
- 2 basic models: Continuous Bag-of-Words (CBOW) and Skip-Gram and various optimisations
- Several variations
Principles
Skip-Gram Model
Maximises probability of identifying context words for each word of the vocabulary \(W\)
\[ \frac{1}{T} \sum_{t=1}^{T} \sum_{-c\leq j \leq c, j\neq 0} \log p(w_{t+j}|w_t) \]
- \(T\) is the size of the vocabulary \(W\), \(w_j\) is the \(j\)-th word of \(W\)
- \(c\) is the size of the context window
Skip-Gram Model
Define conditional probability \(p(w'|w)\) using softmax function:
\[ p(w_O|w_I) = \frac{\exp(v'_{w_O}^{\top} v_{w_I})}{\sum_{i=1}^{T} \exp(v'_{w_i}^{\top} v_{w_I})} \]
Neural Network

Feed Forward
Back-Propagation
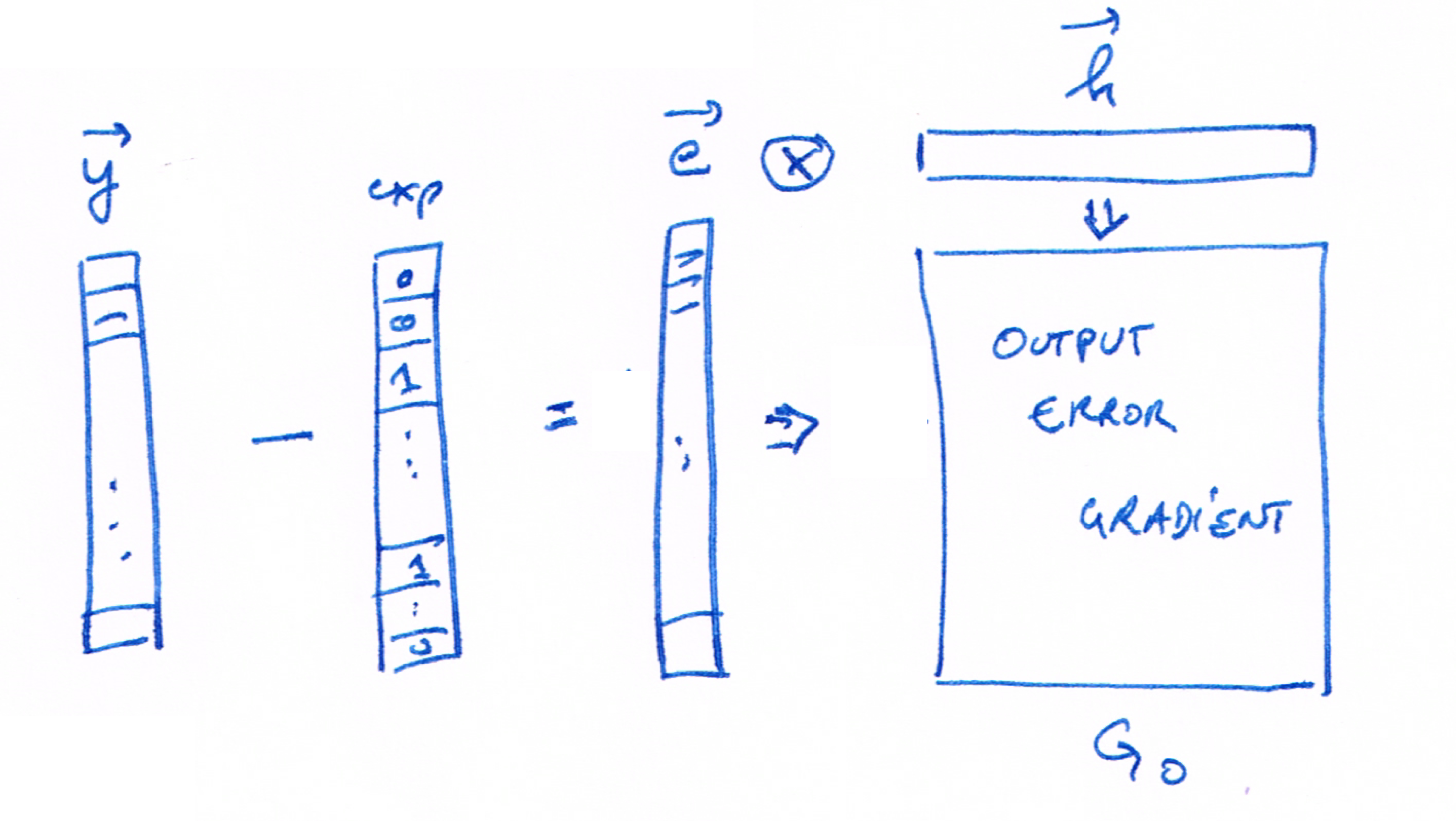
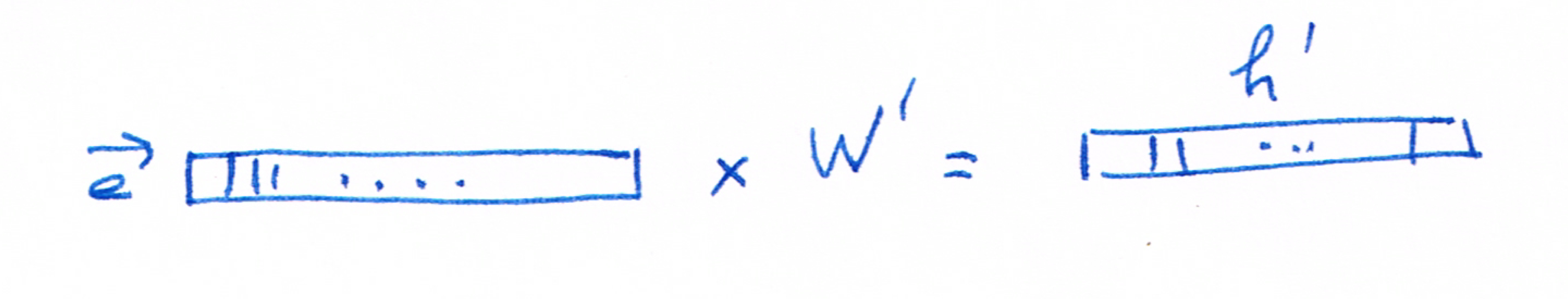
\[ W_{new}' = W' - \alpha G_O \]
\[ w_I_{new} = w_I - \alpha h' \]
(Naive) Code in Haskell
Visualizing word2vec with wevi
Optimizing
Problem
- While correct and straightforward, complexity of basic implementation is huge: For each sample, we need to compute error gradient over \(W'\) which has size \(T x D\).
- Training speed is about \(1/20^{th}\) of reference implementation
- Major contribution of word2vec papers is their ability to handle billions of words…
- How can they do it?
Proposed Optimisations
- Input words sub-sampling: Randomly discard frequent words while keeping relative frequencies identical
- Parallelize training
- Negative sampling
- Hierarchical Softmax
Hierarchical Softmax
Idea: Approximate probability over \(V\) with probabilities over binary encoding of \(V\)
- Output vectors encode a word’s path within the binary tree
- Reduces complexity of model training to updating \(\log(V)\) output vectors instead of \(V\)
Huffman Tree
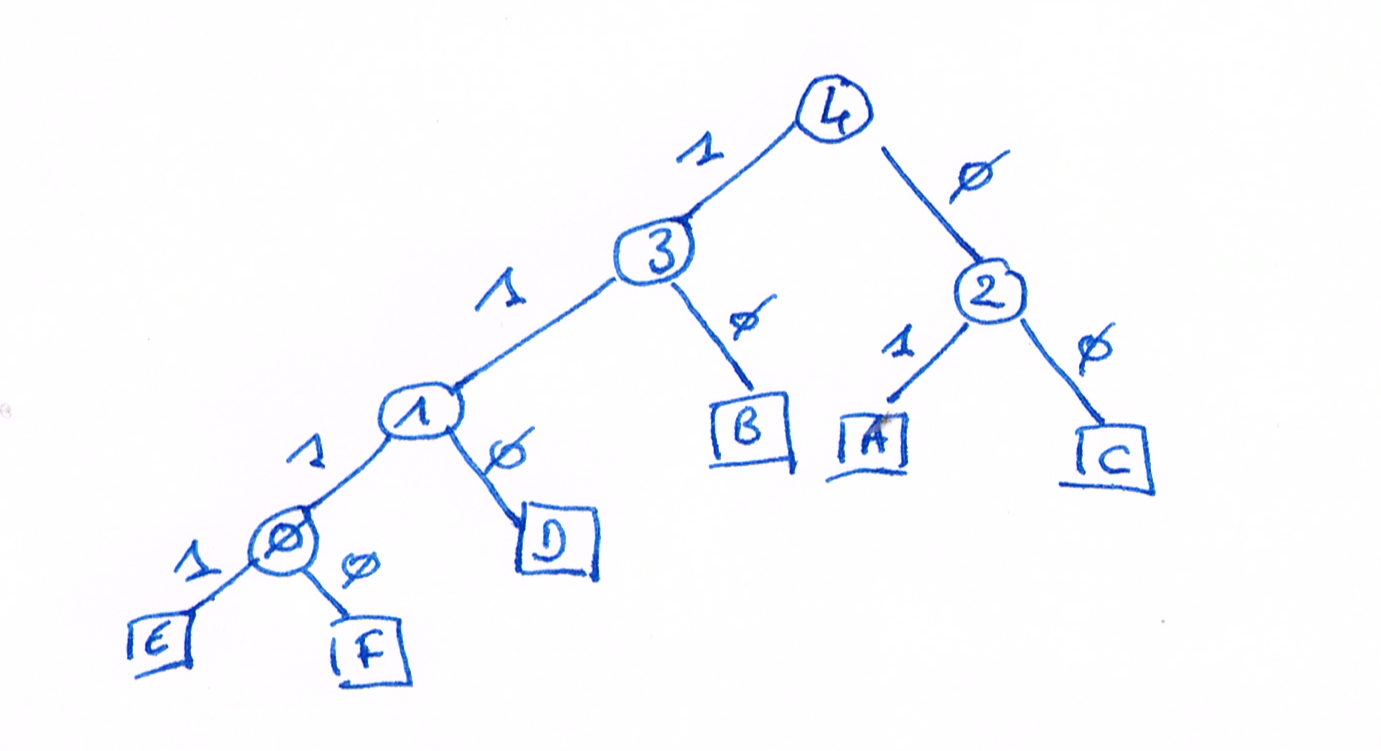
Huffman Tree
- Huffman coding encode words according to their frequencies: More frequent words are assigned shorter codes
- To each word is assigned a path in the Huffman tree which tells, for each node, whether to go left or right
- Each node is assigned a row in the output matrix
Original Code
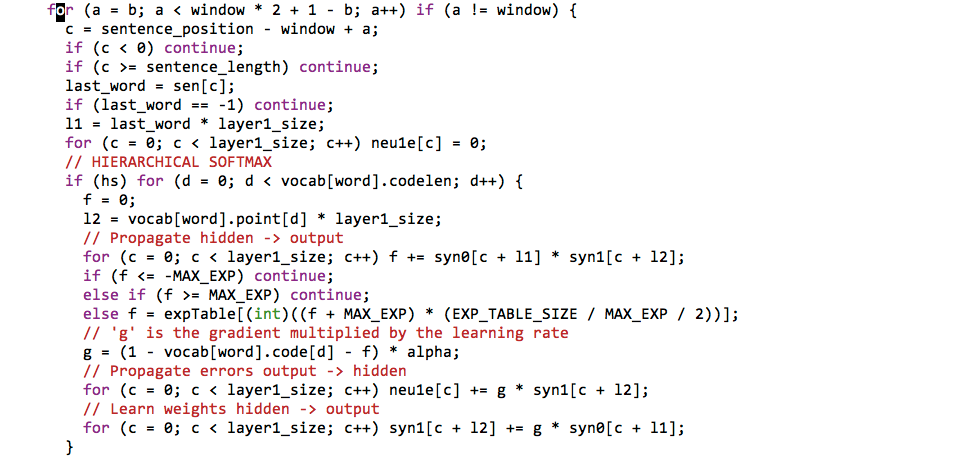
Less naive Haskell Code
More Challenges
Functional Programming
- Haskell is a pure lazy functional programming
- Data is immutable which leads to inefficiencies when modifying very large data structures naïvely
- Need to use mutable data structures and impure code
Data Acquisition
- Retrieve PDFs from Arxiv site
- Extract textual from PDF
- Cleanup text for analysis
Data Visualisation

- Find some way to reduce dimensionality of space
- Most well-known technique is Principal Component Analysis
- Other techniques: t-SNE
Computing PCA
- Standard tool from statistical analysis and linear algebra
- Transform the “basis” of the vector space to order then by decreasing amount of variance
- Select the first 2 or 3 axis to display data on 2D or 3D diagram
Optimizing PCA
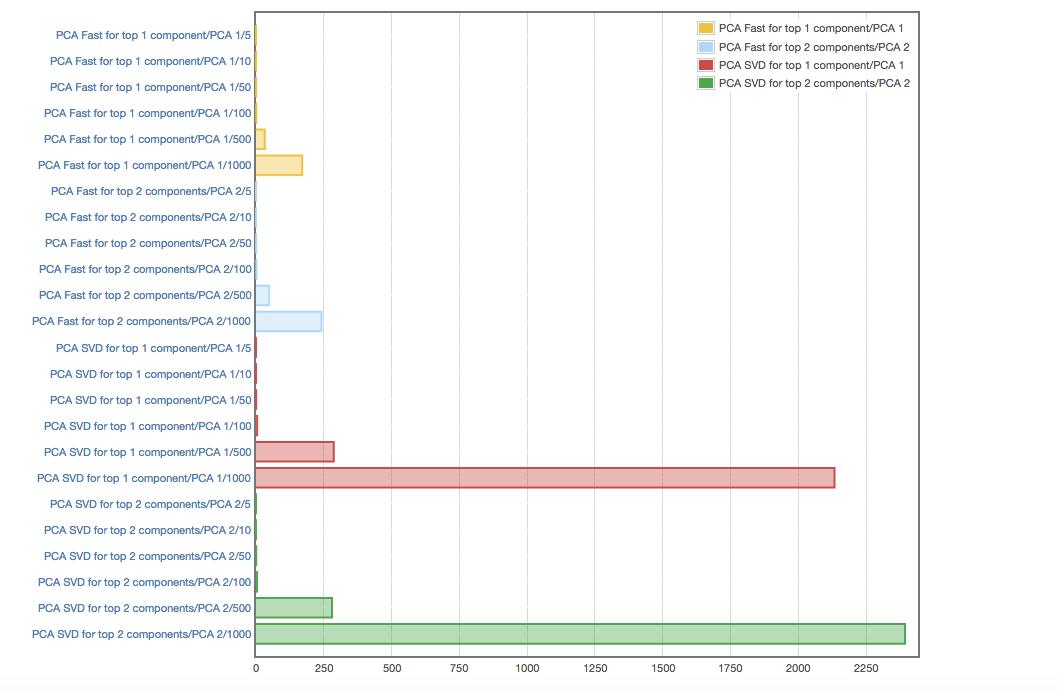
- Textbook computation of PCA means computing full covariance matrix for dataset then eigenvectors of this covariance matrix
- For a 50000 x 200 matrix this is extremely time consuming…
- There exist iterative methods to compute principal components one at a time
Conclusions
Machine Learning is Hard
- In theory: Get some data, find a suitable model, fit model to data using standard logistic regression, use model
- In practice:
- Datasets need to be large which means algorithms need to be efficient
- Efficient algorithms require clever optimisations that are non obvious
- Hard to get “right”…
Machine Learning is Hard (2)
- Still an active research field: Going from research paper to tool is not straightforward
- Reverse engineering code was a painful process
- To really understand what one’s doing requires understanding large chunks of maths: Linear algebra, statistics, numerical analysis, Natural Language Processing…
Machine Learning is Fun
- Stretches your programming skills beyond their limits
- Forces you to tackle new concepts, techniques and algorithms
- Expands knowledge base to cutting edge technology
- Increases his/her love for you
Takeaways
- There is no better way to understand algorithms than to implement them
- For production, don’t roll your own ML engine
unless:
- that’s your core skills domain
- and/or you are prepared to spend time and money
References
- Original word2vec paper
- Word2vec implementations: original C version, gensim, Google’s TensorFlow, spark-mllib, Java…
- Visualizing word2vec and word2vec Parameter Learning Explained
- Implementing word2vec in Python
- Word2vec in Java as part of deeplearning4j (although word2vec is NOT deep learning…)
- Making sense of word2vec
- word2vec Explained
- word2vec in Haskell